¡Magufos!: ¡Que aprenda él mismo! #Cuentos Cuánticos #noticias

Cuentos Cuánticos

Una de las ramas de la robótica que siempre me han encantado es el de la robótica evolutiva. En esta entrada intentaremos explicar por qué es tan atractiva, presentando una de las direcciones en las que se trabaja. Concretamente, veremos cómo se combinan redes neuronales con algoritmos genéticos y aprendizaje por refuerzo. ¡Casi nada!

Pero vayamos por partes. La robótica evolutiva supone un cambio en la forma en la que se programan los robots. Si habéis seguido las entradas de robótica de este blog, os habréis dado cuenta de que en general, los robots se programan a mano para ejecutar ciertas tareas como navegar, coger objetos y manipularlos etc. ¿Qué queremos decir con a mano? Que existe un programador que va escribiendo todas las instrucciones concretas para que el robot pueda hacer lo que hace. Sin embargo, en robótica evolutiva se cambia el enfoque. ¿Por qué deberíamos programar un robot si él mismo puede aprender a hacer las cosas?

Aprendizaje por refuerzo

Para que el robot aprenda, vamos a usar un método de aprendizaje bien conocido por todos: el aprendizaje por refuerzo. Muy llanamente, este tipo de aprendizaje se basa en premiar el comportamiento adecuado y en castigar el comportamiento poco adecuado. Imaginemos por ejemplo, que queremos que nuestro robot levante el brazo derecho cada vez que encendamos una luz. Bien. El robot necesitará un detector de luz para percibirlo y unos brazos. Encenderemos la luz y veremos qué hace el robot. Si no levanta el brazo que nosotros queremos, le mandaremos un refuerzo negativo. Si lo levanta, un refuerzo positivo. Repitiendo este proceso muchas veces, el robot aprenderá que cuando encendamos la luz tiene que levantar el brazo.

Hasta aquí bien, pero ¿cómo se hace eso con un robot? ¿Le tenemos que pegar con un palo cada vez que la pifie? Obviamente no. Esto del castigo y premio en la robótica es mucho más sutil, mucho más matemático. Lo que se hace es definir una función de refuerzo, que no es más que una función matemática que evalúa la acción del robot. Por ejemplo, podemos coger una escala del cero al diez y puntuar las acciones del robot en función a nuestro objetivo. El objetivo del robot será buscar la acción que le haga obtener siempre un 10.

Ya, pero ¿cómo busca el robot esas acciones? ¿Cómo es capaz de decidir qué hacer cada vez que ve una luz? Aquí es donde entran las redes neuronales y los algoritmos genéticos.

Redes neuronales

No es mi intención entrar aquí a explicar en detalle las redes neuronales, las distintas clases de redes que existen, la forma de entrenarlas, etc. Eso, en todo caso, ya lo haremos otro día. Pero en esta entrada sí que veremos algo sobre estas redes, de forma muy simple.

La unidad básica de una red neuronal es la neurona o el perceptrón. Una red neuronal no es más que la unión de varias neuronas. ¿Y qué hace una neurona? Nada del otro mundo: recibe unas señales de entrada, las suma y propaga una señal de salida.

Vamos a detallar esto un pelín más. Las entradas de una neurona son unos números reales. La neurona de la imagen anterior puede procesar por lo tanto vectores de tres dimensiones, ya que tiene tres entradas. Podemos escribir las señales de entrada de una neurona como $\bar{x} = (x_0, x_1, x_2)$ . La salida de la neurona es típicamente un número real. Para obtener dicha salida se aplican dos funciones sobre las entradas:

Función de transferencia: no es más que la combinación lineal de las entradas con unos pesos dados, es decir, $f(\bar{x}) = \bar{w} \bar{x} + b$ . Para nuestro caso anterior, $f(\bar{x}) = w_0 x_0 + w_1 x_1 + w_2 x_2 + b$ . Las $w$ son los pesos de la neurona y ya volveremos a ellas pronto. $b$ representa el parámetro libre, y también veremos su significado en breve.

Función de activación: es una función que calcula una salida en función del resultado de la función de transferencia. Hay muchas clases de funciones de activación. Ahora veremos un ejemplo para entederlo mejor.

Usando las funciones de transferencia y activación, una única neurona es capaz de aprender cosas simples. Imaginad que tenemos dos entradas $(x_0, x_1)$ . Sabemos que dependiendo del valor de esas dos entradas, tenemos una cara o no. Es decir, asumamos – aunque sea mucho asumir – que somos capaces de distinguir una cara solo con dos números reales. En ese caso, una única neurona es capaz de aprender, para cualquier valor de $x_0, x_1$ si es una cara o no. ¿Cómo?

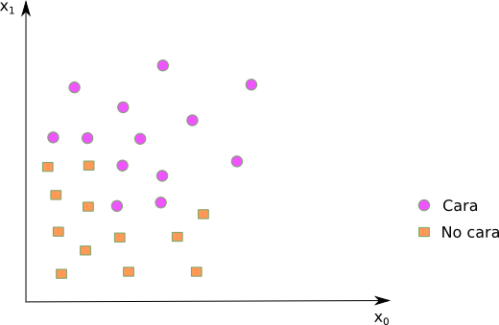
Miremos la gráfica a continuación.

Hemos puesto $x_0$ en un eje y $x_1$ en otro. A continuación, hemos puesto algunos puntos y su clasificación, es decir, si representa una cara o no. Recordad que todo esto es una grandísima simplificación, pero nos ayudará a entender el comportamiento de una neurona.

Una forma simple de ser capaces de distinguir entre caras y no caras, sería trazar una línea recta en el gráfico anterior, de tal forma que las caras queden a un lado de la línea, y las no caras al otro lado. Algo así:

Curiosamente, la función de transferencia que hemos definido antes, no es más que una línea en el espacio de las entradas $f(x_0, x_1) = w_0 x_0 + w_1 x_1 + b$ . Para caracterizar la línea que hemos dibujado, solo hace falta elegir los valores adecuados de $w_0, w_1$ y $b$ . Estos valores se eligen en un proceso de entrenamiento que por ahora, vamos a dejar en el aire. Pero vaya, nuestra simple neurona es capaz de aprenderse esta línea que distingue a las caras de las no caras. Si enchufamos esta función de transferencia en una función de activación que diga que si un punto dado $(x_0, x_1)$ está por encima de la línea aprendida, entonces ese punto es una cara, ya tenemos un clasificador lineal. Nuestra neurona sabe distinguir entre caras y no caras.

Ahora que sabemos la capacidad de una neurona, pensemos en una red neuronal. Tenemos muchas neuronas, cada una de ellas capaz de aprender un clasificador lineal. Las salidas de unas se convierten en las entradas de otras, tejiendo una red todo lo compleja que queramos. Pero aquí hay un problema: si enganchamos entre sí millones de neuronas de la forma que hemos descrito hasta ahora, nuestra red neuronal no será más que otro clasificador lineal. Dicho más formalmente, la composición lineal de un número arbitrario de funciones lineales, resulta en otra función lineal. Y una función lineal no es capaz de aprender relaciones complejas entre entradas y salidas. ¡Vaya fiasco!

Hay una solución muy simple a este problema. En vez de usar la función de activación que hemos descrito (que es lineal), usemos una función no-lineal. En redes neuronales una de las funciones más usadas es la función sigmoide:

$S(x) = \frac{1}{1 + e^{-x}}$

Esta función tiene este aspecto si lo ponemos en un gráfico:

Vamos, que según el valor de la función de transferencia para un punto dado, la función sigmoide nos dará el valor que aparece en el gráfico para ese punto dado. Introduciendo una función de activación no-lineal en cada una de las neuronas, ahora nuestra red neuronal es capaz de hacer cosas mucho más chulas.

Redes feedfoward

Ya sabéis que a los informáticos nos mola eso de usar términos ingleses. Una de las redes neuronales más simples es la llamada feedforward. La podemos ver en la siguiente imagen:

Tenemos 3 neuronas de entrada, 4 neuronas en la llamada capa oculta y 2 neuronas de salida. Todas las neuronas de una capa están conectadas con todas las neuronas de la siguiente capa. Cada neurona recogerá las entradas que le lleguen, aplicará la función de transferencia con los pesos concretos y propagará la salida a las siguientes neuronas usando la función de activación – en nuestro caso, la función sigmoide -. Sencillo, ¿verdad?

Lo más alucinante de esta red neuronal feedforward es que según matématicos sesudos, es capaz de aproximar con un error arbitrariamente pequeño cualquier función no-lineal entre las entradas y las salidas. A esto le llaman el teorema de aproximación universal. Poniéndolo en palabras más de andar por casa, quiere decir que una red feedforward, con una única capa oculta y un número finito de neuronas, es capaz de aprender cualquier relación entre unas entradas y unas salidas. En la práctica, hay relaciones que se aprenden mejor añadiendo más capas ocultas, y esto nos llevaría a tratar el tema del tan famoso deep learning. Pero por ahora, dejemos las cosas como están: una única capa oculta nos sirve para lo que queremos.

¿Y todo esto para qué?

Llevemos esto de las redes neuronales a nuestro problema anterior del robot que tenía que levantar el brazo derecho cuando se encendía una luz. Hemos comentado que el robot necesitaba un detector de luz. Dicho detector, seguramente, nos dará la intensidad de la luz que percibe, en una unidad adecuada. Ese valor de intensidad será la entrada a nuestra red. Las salidas serán los comandos que se necesiten para mover los motores de los brazos robóticos. Nos da igual cómo son esos comandos. Habrá unos valores reales que hagan que los brazos se muevan de diversas formas. Pues nada, ya tenemos nuestra red feedforward que es capaz de controlar los movimientos de unos brazos en función de la intensidad de la luz.

Como la red neuronal es capaz de aprender cualquier relación entre las entradas (intensidad de la luz) y las salidas (comandos de los brazos), eso quiere decir que existen unas combinaciones de pesos en nuestra red neuronal que harán que el robot alce el brazo derecho cuando encendamos la luz, y no haga nada cuando se apaque. La clave ahora es saber cómo buscar los valores de todos esos pesos. Y es allí donde van a surgir los algoritmos genéticos y el aprendizaje por refuerzo.

Pero todo eso lo dejaremos para la siguiente entrada. Al final me he enrollado mucho con el tema de las redes neuronales y será mejor dejar esta entrada aquí mismo. En la(s) siguiente(s) entrada(s) veremos cómo los algoritmos genéticos combinados con aprendizaje por refuerzo nos sirven para buscar los valores de los pesos de la red neuronal. Y os pondré algun que otro vídeo guay -refuerzo positivo ;) -

Nos seguimos leyendo…

Archivado en: ingeniería, inteligencia artificial, matemática, robótica

Fuente
Cuentos Cuánticos / facebook.com
Un sitio donde los cuentos de ciencia están contados y no contados al mismo tiempo