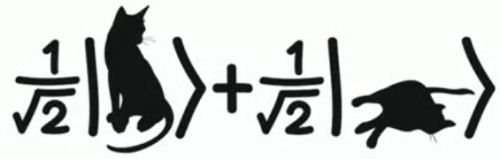Hoy ha caído en mis manos el artículo:
El problema de la cuántica y su interpretación
En mecánica cuántica se describen los estado de un sistema, generalmente se les denomina funciones de onda 
Una de las características esenciales de la mecánica cuántica es que la función de onda o estado cuántico de un sistema puede ser una combinación de estados que dan resultados experimentales excluyentes.
Aquí viene el sacrosanto ejemplo del gato de Schrödinger:
El gato se mete en una caja con un elemento que tiene una probabilidad del 50% de matarlo. La cuántica nos dice que mientras que no abramos la caja y observemos al gato este está en un estado superpuesto, combinado, del gato vivo y el gato muerto:
Ese estado hay que leerlo del siguiente modo:
- El estado del gato
está compuesto por la superposición de dos estado,
y $|Gato_{muerto}\rangle$.
- La mecánica cuántica nos dice que cuando abramos la caja lo veremos o bien vivo, o bien muerto. Estas son propiedades del sistema gato mutuamente excluyentes en nuestro nivel clásico, donde operan las leyes de Newton y no la mecánica cuántica. Pero además nos dice que la probabilidad de ver una cosa u otra nos la marca el cuadrado del coeficiente de cada estado de la combinación. En este caso los cuadrados son 1/2, es decir, 50% de probabilidad.
Un problema gordo es que, aunque la cuántica vive bien con este tipo de estados, nosotros no podemos ver sistemas en combinaciones de estados excluyentes. Vemos al gato vivo o al gato muerto pero no en una combinación. Eso quiere decir que cuando hacemos la medida del estado superpuesto solo nos quedamos con una de las partes, la otra desaparece. Ese hecho se denomina colapso de la función de onda y no tenemos ni idea de cómo o por qué pasa.
Por supuesto, todo esto del gato solo es un ejemplo extremo, muy bueno, pero solo un ejemplo. En cuántica podemos trabajar con sistemas que están en estados combinados de diferentes energías aunque nosotros solo podemos ver que está en una única energía cuando la medimos en el sistema. O el sistema puede ser descrito como una combinación de distintas ubicaciones espaciales aunque cuando medimos la posición del sistema nos da un valor. Todo lo que podemos decir es con qué probabilidad lo encontraremos en un estado u otro de la combinación de estados inicial.
Explicaciones se han propuesto muchas para todo esto, ninguna de ellas plenamente convincente o que haya dado lugar a la posibilidad de comprobarla experimentalmente. La de hoy es otra más, con cosas buenas y cosas malas. Pero antes de profundizar en la explicación de hoy hay que introducir un poco la explicación de los muchos mundos de Everett.
Muchos mundos para Everett
Everett se aplicó a intentar explicar el colapso de la función de onda y lo que propuso es que el colapso en realidad no se daba. La función de onda nunca colapsa, sino que en el acto de medir el universo al completo se desdobla en tantas ramas como estados tenga la combinación. En el caso del gato, al abrir la caja el universo se desdobla en dos ramas, pero pudieran ser muchas más dependiendo de la combinación de estados.
Entonces lo que ocurre no es colapse la función de onda sino que nosotros percibimos el estado que está en la rama que nos ha tocado pero habrá otra copia de nosotros que perciba lo contrario. Es decir, al abrir la caja el universo se desdobla en dos partes:
- En una vemos el gato vivo.
- En otra vemos el gato muerto.
- En todas las ramas hay una copia de todo, nosotros, la caja, el gato, etc, y no notamos el desdoblamiento del universo.
El universo sufrirá tantos procesos de división como medidas hagamos sobre estados cuánticos superpuestos y en cada una de ellas se dividirá en tantas ramas como estados que formen la combinación.
No vamos a discutir aquí los problemas de esta interpretación, pero por mencionar unos pocos:
- ¿Cómo se divide el universo?
- ¿Qué es medir cuánticamente? ¿Cómo sabe el universo que hemos hecho una medida?
- ¿Cómo de rápido es el proceso?
- ¿Es reversible o irreversible?
- Etc.
Lo importante aquí es que un punto esencial en la interpretación de los muchos mundos de Everett cada rama separada del universo, potencialmente infinitas, no interactúa nunca jamás con el resto de ramas del mismo. Se separan y en paz, adiós muy buenas.
Las bases del artículo de hoy
En el artículo que traemos hoy se dan una serie de ingredientes básicos:
- Hay muchos universos en los que las leyes de la física son pura y simplemente las leyes de Newton, es decir, la física clásica, la no cuántica.
- En esta imagen se parte de un número inmenso pero finitos de dichos universos.
Ahora hay que responder a unas cuantas preguntas:
¿De dónde salen las leyes de la cuántica?
Dicen que de la interacción entre esos universos. La interacción es de tipo repulsivo siempre y cuando los universos que entren en juego estén en configuraciones casi idénticas. Vamos, es una interacción que repele la igualdad de universos.
Si hay universos en configuraciones muy diferentes, estos ni se influyen ni se molestan.
¿De dónde salen las probabilidades cuánticas?
Como hemos dicho cuando tenemos un estado superpuesto la cuántica nos dice que probabilidad hay de medir cada estado de la composición. En el caso del gato tenemos 50% para el gato vivo y 50% para el gato muerto. Esas probabilidades nos la da la cuántica.
En el modelo expuesto en el artículo lo que nos dice es lo siguiente:
- Las probabilidades aparecen porque nosotros no sabemos en qué universo de todos los posibles estamos. Así que hay universos en los que el gato está vivo y universos en los que el gato está muerto. En el experimento del gato, tal y como está diseñado, hay el mismo número de universos en el que el gato está vivo que de universos en el que está muerto, por lo tanto la probabilidad de que lo veamos vivo o muerto en el nuestro es del 50%.
- Si creamos un estado que tiene probabilidad del 70% de estar vivo el gato y 30% de estar muerto significa que hay muchos más universos en los que el gato está vivo y muchos menos en los que está muerto.
Vamos, que simplemente es cuestión de números de universos.
¿Han verificado en el artículo que se recupera la cuántica?
No, como dicen en el propio artículo. Lo que sí han confirmado es que dependiendo del número de universos se puede aproximar mucho el comportamiento cuántico de los sistemas. Es una forma de emular la cuántica metiendo muchos universos de por medio.
Han comprobado que se pueden aproximar algunas cosas interesantes como:
- El teorema de Eherenfest.
- Las relaciones de indeterminación de Heisenberg.
- La dispersión del paquete de ondas.
- Cálculo de estados de mínima energía de sistemas muy simples como osciladores.
- Etc.
Sin embargo, la única forma de recuperar exactamente la cuántica es introduciendo infinitos universos en el juego. Esto es un poco insastifactorio, la cuántica es una de las teorías mejor contrastadas experimentalmente, así que no basta con dar aproximaciones, hay que recuperar todos sus resultados y encontrar otros para tener una teoría que compita con ella.
Hay un hecho curioso, explican el efecto túnel como el efecto de la interacción entre dos universos de esos.
Efecto túnel
En cuántica hay veces en las que una partícula descrita por un estado cuántico puede hacer algo para lo que se le supone que no tiene energía suficiente. Por ejemplo, una partícula lanzada contra una barrera de una determinada altura no podrá saltarla si no tiene la suficiente energía, llegará a la barrera y rebotará. Pero eso es a nuestra escala.
Si estudiamos el mismo caso pero con un sistema cuántico nos llevaremos una sorpresa. La cuántica nos dice que el sistema rebotará en la barrera muchas veces pero que hay una pequeña probabilidad de que la traspase y aparezca al otro lado. Eso es lo que se conoce como efecto túnel.
La onda azul es la representación de la descripción cuántica de la onda. Inicialmente está en la región 1 y se encuentra con la barrera. La energía no es suficiente como para pasar a la región 3, la onda azul no tiene la altura necesaria para saltar la barrera. Sin embargo, hay una pequeña probabilidad de que pase al otro lado, región 3, y eso se ve en que la curva azul en dicha región aumenta de 0 a un valor apreciable. Evidentemente, en la región 1 la probabilidad de encontrar la partícula es mayor que en la 3.
En el artículo explican el efecto túnel del siguiente modo:
- Tenemos dos universos en los que la partícula se dirige hacia la barrera con una energía insuficiente para saltarla.
- Debido a que en dichos universos la configuración es parecida ocurre que hay repulsión entre ellos.
- La energía de repulsión puede ser absorbida por la partícula en un universo y acelerar para tener la energía necesaria para saltar la barrera.
Por tanto, el efecto túnel sería una manifestación de la repulsión entre universos parecidos.
Las pegas al artículo
¿De dónde salen esos universos? ¿Cuántos hay?
¿Por qué hay una interacción repulsiva entre universos en configuraciones parecidas? ¿Quién rige dicha interacción? ¿De dónde surge?
- Lo que recupera el modelo no es la mecánica cuántica sino una aproximación a la mecánica cuántica. Para recuperar la mecánica cuántica hay que considerar infinitos universos.
- El modelo se circunscribe a mecánica cuántica no relativista, es decir, no explica el origen de la antimateria, del espín, de las partículas elementales que conocemos del modelo estándar.
- El modelo no dice nada de procesos tales como entrelazamiento o teleportación, que son elementos esenciales de la mecánica cuántica verificados experimentalmente.
- El modelo no calcula el espectro no relativista del átomo de hidrógeno.
Lo que me gusta
Lo que me gusta del artículo es:
- Reconocen que es un modelo muy preliminar.
- Aceptan que no es una alternativa viable, por ahora, a la cuántica pero que es un marco de aproximación a la misma.
- Plantean la necesidad de investigar los temas oscuros que he comentado en los puntos anteriores.
Así que podría ser un divertimento y una forma de introducir, jugando, la mecánica cuántica. Tal vez el modelo sea un buen método de aproximar sin mucha parafernalia efectos cuánticos sabiendo que solo es una herramienta para ello.
Por ahora, la cuántica no tienen rival.
Nos seguimos leyendo…
Archivado en: mecánica cuántica Tagged: colapso de la función de onda, interpretaciones de la mecánica cuántica, mecánica-cuántica, superposición
Fuente
Cuentos Cuánticos / facebook.com
Un sitio donde los cuentos de ciencia están contados y no contados al mismo tiempo
