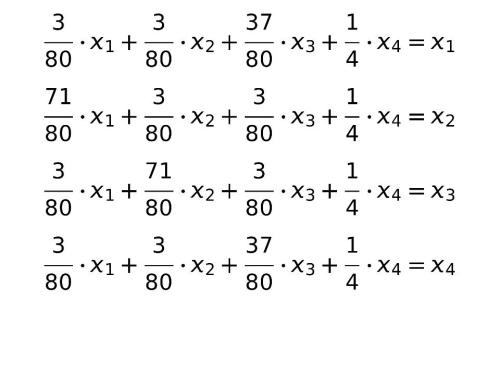Casi seguro que has utilizado algún buscador de internet alguna vez. Es incluso posible que hayas llegado a esta página a través de uno de ellos. Y muy posiblemente, el buscador elegido para la tarea haya sido Google.
¿Te has preguntado alguna vez cómo funciona Google? ¿Cómo posiciona las páginas para mostrarlas antes o después en una lista de resultados de búsqueda? No, no es magia, lo que hay detrás de todo eso son matemáticas.
Pues en esta entrada vamos a construir un buscador en una internet de mentira. Pasen y vean.
Mi internet
Mi internet solo tiene cuatro páginas, sí lo sé es un internet modesto pero estamos empezando. Las páginas son:
Página 1: quemedejes.com
Página 2: brotesverdes.org
Página 3: yonohesido.com
Página 4: blackcard.es
Algunas páginas de estas tienen enlaces para ir a otras de la internet de CC. Los enlaces son los siguientes:
quemedejes.com tiene un enlace a brotesverdes.org
brotesverdes.org tiene un enlace a blackcard.es
blackcard.es tiene dos enlaces, uno a quemedejes.com y otro a yonohesido.com
yonohesido.com no tiene enlaces a ninguna página.
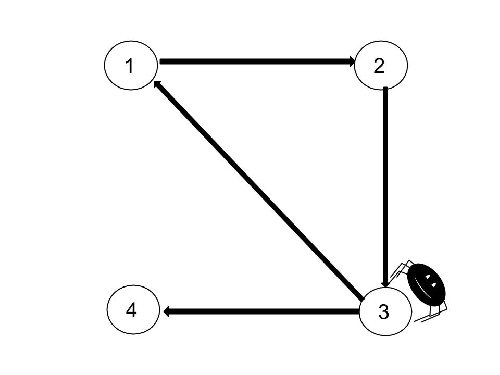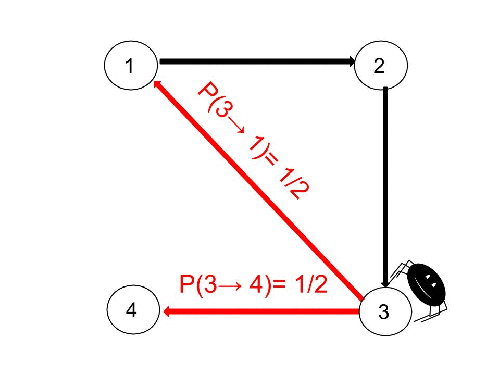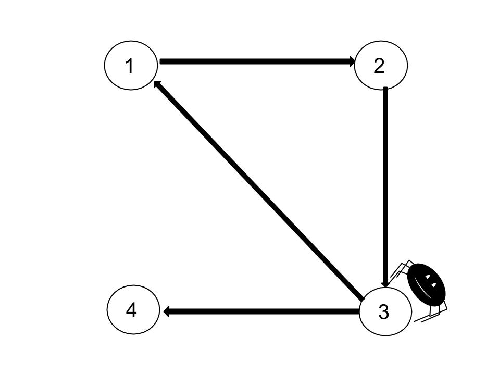
Tal vez se vea más claro en la siguiente imagen:
Nuestra internet con los enlaces de unas páginas a otras indicados.
Esto que tenemos aquí no es más que lo que se conoce en matemáticas como un grafo. Un grafo es un conjunto de puntos denominados nodos y una serie de líneas entre ellos denominadas aristas que aparecen siempre que entre dos nodos haya una relación establecida. En este caso, la relación es que una página apunte a otra con un enlace. Dado que el hecho de que la página A apunte a la página B no implica el caso inverso, que B apunte a A, este grafo nos da la relación de quién sigue a quien, se denomina grafo dirigido.
Así, desde el punto de vista formal nuestra internet no es más que este grafo dirigido:
Grafo dirigido que representa nuestra internet.
Ya hemos dado el primer paso para describir matemáticamente nuestra internet. Ahora tenemos que averiguar qué página es más importante para que cuando hagamos una búsqueda esta aparezca primero.
Una forma menos amigable de mi internet
Acabamos de escribir nuestra internet en forma de grafo dirigido pero si queremos ver las tripas y poder sacar conclusiones tenemos que dar contenido a ese grafo de forma que podamos hacer cálculos.
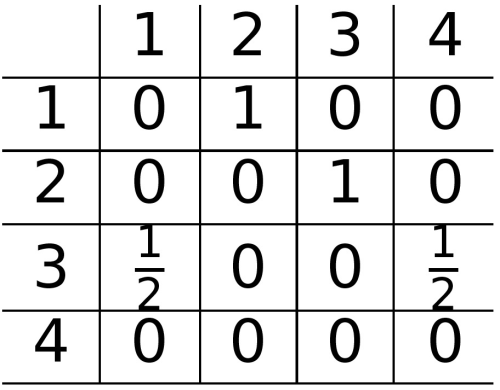
Todo grafo se puede poner en forma de tabla. Lo único que tenemos que hacer es poner tantas filas y columnas como nodos tenga nuestro grafo. En nuestro caso tendremos una entrada de cuatro filas y de cuatro columnas:
Una tabla así hay que saber leerla. Para nosotros la filas indican los nodos de partida y las columnas los nodos de llegada en términos de la relación una página enlaza a otra.
Ahora hay que dar algunas reglas para poder rellenar la tabla con significado.
- Una página no se puede enlazar a sí misma. Por lo tanto a los huecos correspondientes a los términos 1–>1, 2–>2, 3–>3, 4–>4, les asignamos un cero.
- Ahora cuando una página enlaza a otra le ponemos un 1 dividido por el número total de links que tiene dicha página hacia otras externas.
La tabla que describe nuestro grafo queda:
Así que lo que hemos hecho es describir el grafo a partir de una tabla. Ambas cosas son equivalentes, es decir, tienen la misma información, solo que en una representación los aspectos cualitativos están más de manifiesto y en la otra los aspectos más cuantitativos.
De hecho, dado que el sentido de lectura está claro, podemos simplificar la tabla y trabajar con esta otra representación:
Esto es lo que se conoce como matriz, que como hemos visto no es más que una tabla de números.
¿Qué significan esos números? Bueno, eso tendrá que esperar un poco, ahora lo que vamos es a presentar a la protagonista de nuestro buscador.
Amaestrando arañas
Nuestra araña buscadora
Sí, para poder buscar en nuestra internet hemos de conocerla muy a fondo. Para ello lo que hacemos son programas de ordenador que rastrean nuestra red, por ello, en un alarde de originalidad, los llamaremos arañas.
La araña puede aparecer en nuestra internet de manera aleatoria. Simplemente selecciona una dirección de un listado y se sitúa ahí. Luego, con cierta probabilidad elegirá algún enlace de la página en la que se encuentre y se irá a la página enlazada. En la nueva página vuelve a buscar todos los enlaces y selecciona uno para visitar esa nueva dirección. Este proceso lo hace tantas veces como queramos.
Evidentemente, tenemos varias posibilidades de paseo dependiendo de en qué página aparezca. Vamos a describir esas posibilidades con nuestro internet de juguete.
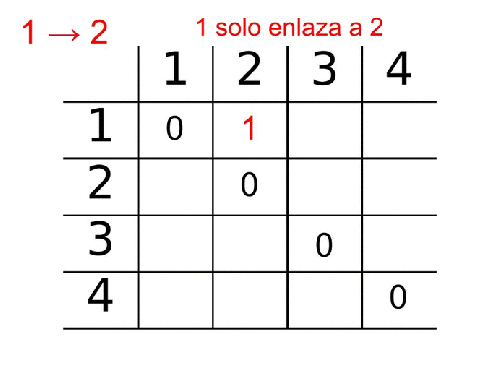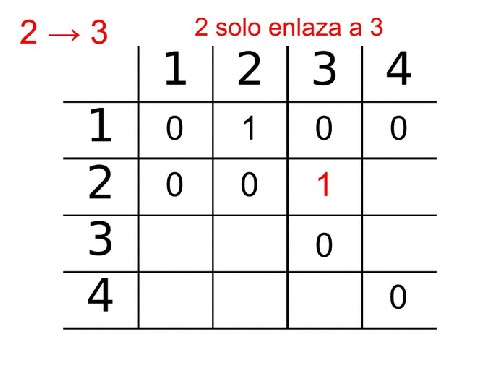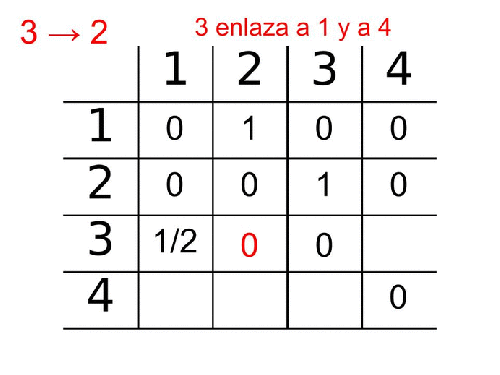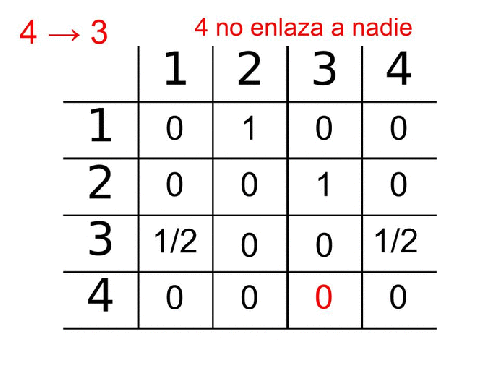
La araña aparece en la página 1 (quemedejes.com)
La araña, cumplidora ella, busca todos los enlaces y el único que encuentra es el que apunta a la página 2. Así que con una probabilidad del 100% se irá a la página 2. Si redefinimos las probabilidades para que tengan valores entre 0 y 1, la probabilidad de que la araña vaya a 2 partiendo de 1 tiene un valor 1 (100%). Evidentemente, la probabilidad de ir a la página 3 o 4 desde 1 es 0.
La araña aparece en la página 2 (brotesverdes.org)
Si aparece en el nodo 2 la probabilidad de ir al nodo3 también vale 1 ya que la página 2 solo enlaza a la página 3.
La araña aparece en la página 3 (blackcard.es)
En este caso la araña detecta que hay dos enlaces, uno a la página 1 y otro a la página 4. Así que saltará al nodo 1 o al nodo 4 con una probabilidad de 1/2, es decir, con una probabilidad del 50%.
La araña aparece en la página 4 (yonohesido.com)
Si la araña aparece en el nodo 4 no puede ir a ningún sitio ya que la página 4 no enlaza a nadie.
Parece que nuestra araña está un poco perdida ahí. Algo tendremos que inventar para que pueda seguir con su trabajo. Pero antes de eso, volvamos a mirar la tabla que construimos del grafo asociado a nuestro internet.
La tabla y la araña
Quizás esta sección de la entrada no haga falta porque ya hayáis detectado por dónde van los tiros. Sí, la araña se mueve por el grafo en función de probabilidades que podemos leer de nuestra tabla. Mirad este caso:
La fila 1 de la tabla nos dice hacia donde apunta la página 1. De nuestra internet podemos saber mirando dicha tabla que la página 1 solo apunta a la página 2. Por tanto, al único sitio que podemos ir navegando entre páginas si estamos en la página 1 es a la página 2. La probabilidad de ir de 1 a 2 es 1.
Así pues, en la tabla, o en el formato de matriz, lo que tenemos son las probabilidades de ir aleatoriamente a una página cualquier a partir de una dada. Ese es el significado que nos interesa de nuestra tabla. ¿A que ahora parece diferente dicha tabla?
¿Qué hacemos si llegamos a un callejón sin salida?
Hemos detectado que en nuestro internet hay un callejón sin salida. La página 4 no apunta a nadie y el trabajo de la araña no puede seguir. Esto se ve en la tabla/matriz porque hay toda una fila llena de ceros.
¿Acaso aquí se acaba nuestra aventura? Pues pudiera ser, pero no, hemos olvidado algo.
Tenemos que decirle a la araña, en su programación que siempre hay posibilidad de ir a cualquier otra página de internet aunque no haya enlaces a ella en la página que nos encontremos. Para algo se inventó la barra de direcciones. Uno podría simplemente teclear la dirección de cualquier página y dirigirse hacia ella.
Llegados al caso de encontrar un nodo insociable como el nodo 4 enseñamos (programamos) a nuestra araña a que teja todas las conexiones posibles partiendo de 4. Entonces nuestra araña imagina que la red es en verdad de este tipo:
Como vemos, nuestra araña teje hilos virtuales de conexiones entre 4 y todas las demás páginas, y además añade la posibilidad de que el navegante se quede en la página 4. Por lo tanto, la tabla del grafo en este caso tendrá la forma:
O en forma de matriz:
Es importante notar que la suma de todos los elementos de cada fila nos da 1. Es decir, que todos los elementos de la tabla/matriz se pueden considerar probabilidades como habíamos deducido del comportamiento de nuestra araña.
Internet la usan personas
Si nuestra internet solo fuera usada por arañas que se mueven aleatoriamente por las páginas según hemos indicado aquí hubiera acabado nuestra historia y ahora deberíamos de dar la receta para seleccionar los nodos más importantes. Es decir, tendríamos que decir qué páginas tienen más peso en la red y por lo tanto aparecerán antes en las búsquedas.
Sin embargo, internet es usada por personas. Y las personas pueden tener cierta preferencia a visitar páginas conocidas de antemano y a no seguir los enlaces de las páginas en las que se encuentren.
Para modelizar estas tendencias personales hemos de modificar un poco nuestra tabla. Para ello seguiremos los siguientes pasos:
- La tendencia a seguir enlaces de la página en la que estamos es alta pero no es seguro que se sigan. Entonces vamos a meter un factor multiplicando a cada elemento de la tabla que tenga valores comprendidos entre 0 y 1. Dado que la tendencia a seguir enlaces es alta vamos a elegir el valor 0.85, o lo que es lo mismo 85/100. Así que nuestra tabla quedará:
Lo que en foma de matriz queda:
Fijaos que ahora la suma de los elementos de cada fila no da 1. Por lo tanto, las cantidades que hay ahí no se pueden considerar todavía probabilidades como sería deseable.
- Lo que ha pasado es que hemos pasado por alto una cuestión esencial. Si aceptamos que los navegantes seguirán los enlaces de las páginas que visiten con una tendencia alta, del 0.85, también tenemos que aceptar que saltarán a otras páginas con una tendencia de (1 – 0.85), es decir, 0.15=15/100. Por tanto, un navegante podrá saltar a cualquier otra página de las 4 que hay , por lo que tiene una probabilidad cada una de ser elegida de 1/4, con una probabilidad del
. Entonces, ahora tenemos que sumar esa cantidad a todos los elementos de la tabla, porque esa es la probabilidad de que se llegue a esa página desde cualquier otra a través de una decisión personal del navegante.
Que en formato de matriz quedaría tan bonita como:
Podemos simplificar los números, la última fila es muy fácil porque dividimos arriba y abajo por 100 todos los elementos. En las restantes dividimos arriba y abajo por 5. Si hacemos eso la matriz queda:
Ahora sí que la suma de todos los elementos pertenecientes a una fila da como resultado 1. Ahora sí que podemos pensar que esas son las probabilidades que combinan la estructura natural de la red de nuestra internet (el grafo) y los gustos personales de los navegantes (una aproximación).
Vale, pero… ¿qué página es más importante?
Esa información está escondida en esa tabla/matriz. Y para sacarla a la luz hemos de hacer un cálculo más, en realidad resolver un conjunto de ecuaciones.
Para hacer que la matriz escupa qué página es más importante vamos a inventar una serie de valores desconocidos, 
La forma de sacar a la luz esta información es haciendo este cálculo:
¿Cómo se hace eso?
Sigue estos pasos:
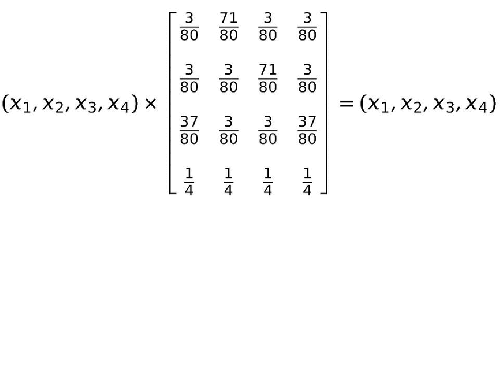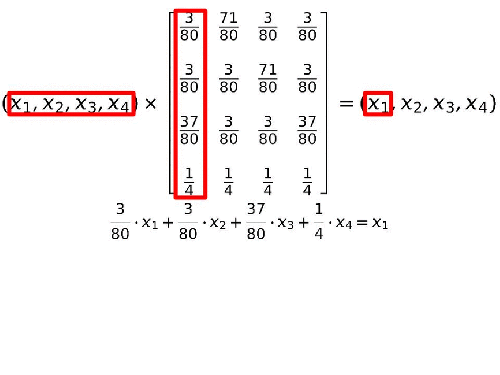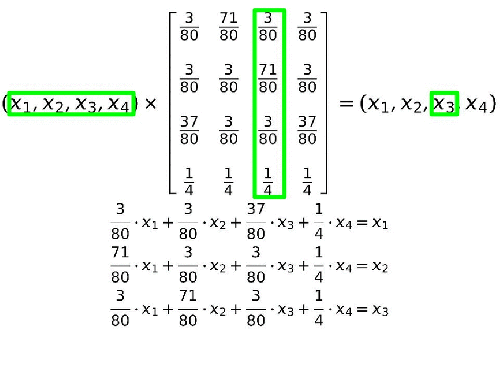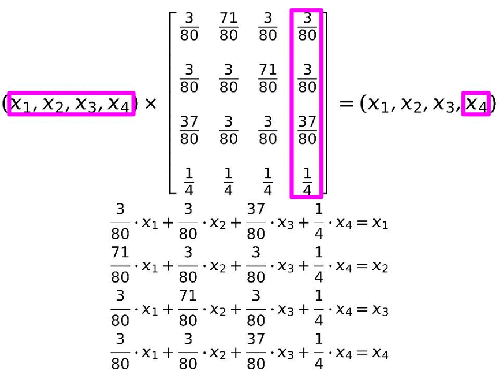Para llegar esto hay que multiplicar cada elemento de las incógnitas por cada elemento de cada columna de nuestra tabla (una cada vez) y sumar los resultados. Esas sumas de números por incógnitas se iguala a cada elemento de la fila del término de la derecha de la igualdad.
Al final lo que tenemos es que resolver un sistema de cuatro ecuaciones con cuatro incógnitas.
No voy a explicar como resolver estas cuatro ecuaciones que conforman el sistema. Simplemente voy a dar la solución y comprobaremos en un caso que se cumple la igualdad (el resto de casos lo podéis comprobar vosotros).
La solución a este sistema viene dada por:
Vamos a comprobar que esa solución funciona. Para ello tomaremos la primera ecuación, sustituiremos los valores de cada una de las incógnitas y miraremos que el resultado sea lo que esperamos.
Esto lo podemos hacer en cada una de las ecuaciones y veremos que obtenemos el resultado requerido.
¿Qué significan los valores 
Esa es la importancia que tiene el nodo en su red. A mayor valor, mayor importancia en la red.
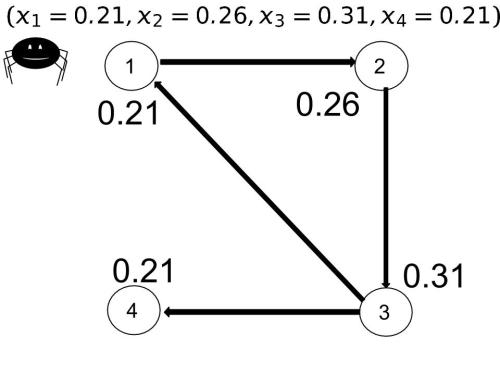En nuestra internet el nodo más importante es el 3, es la página que más tráfico puede generar ya que apunta a dos páginas. Las páginas 1 y 4 tienen el mismo peso en la red, curioso. Y la página 2 tiene mayor importancia que 1 y 4 pero menor que 3.
¿Qué es esto que hemos hecho?
Hemos calculado el pageRank al estilo de Google para nuestro internet. Google es una máquina que hace justamente esto, tiene arañas que visitan páginas y estudian la conectividad de unas con otras y le asignan pesos de importancia en la red, el denominado pageRank.
Por supuesto que Google hace todo esto de forma espectacular porque abarca toda la internet real.
Simulación del grafo de internet
Además tiene herramientas secretas. No se conoce como asigna las probabilidades de visita asociadas a cada navegante que nosotros hemos supuesto que eran (1/número de nodos, 1/4) para tener en cuenta cuando un navegante no sigue los enlaces de la página que está visitando.
Por supuesto, en Google pueden tocar los números asociados con el pageRank, por ejemplo si pagas, para posicionarte mejor en las búsquedas.
Engañar a Google cada vez es más difícil, no es buena idea poner muchos enlaces a la misma página desde la tuya porque entonces os penalizan. Así acaban con el linkspam. Y encima, ahora tienen en cuenta tus búsquedas anteriores y tus visitas para darte un resultado de búsqueda personalizado. Si te has fijado si dos personas hacen la misma búsqueda conectados a sus cuentas de Google obtienen diferentes resultados. En fin…
Para profesores
En este tema se han tocado elementos de:
- Álgebra lineal básica de matrices y resolución de sistemas de ecuaciones.
- Para calcular el pageRank en realidad hay que calcular los autovalores asociados a la matriz del grafo cuando has introducido las preferencias de los navegantes. Así se puede introducir el tema de diagonalización y de análisis espectral de matrices.
- Las matrices empleadas son matrices estocásticas que tienen un papel fundamental en el estudio de procesos de Markov. Este es un buen tema para introducir tales procesos y temas más avanzados de probabilidad.
La moraleja de todo esto es que hay dos señores que pasaron de multiplicar y diagonalizar matrices (con algunas cosas más) a dominar el mundo, literalmente. Y se puede decir que todo ha sido gracias a la matemática.
Tengo que decir que la inspiración para esta entrada me vino cuando leí a @ClaraGrima en CienciaXplora:
Referencias
Si quieres profundizar en este tema:
Mathematical properties and Analisys of Google’s PageRank
The mathematics behind Google’s PageRank
Y no puede faltar la cuántica a esta fiesta:
Quantum Google in a Complex Network
Algún día hablaremos de esto del Google y la cuántica.
Nos seguimos leyendo…
Archivado en: redes sociales, teoría de grafos Tagged: autovalores, autovectores, google, grafo, grafo dirigido, matriz de adyacencia, matriz estocástica, pagerank, proceso de Markov
Fuente
Cuentos Cuánticos / facebook.com
Un sitio donde los cuentos de ciencia están contados y no contados al mismo tiempo
